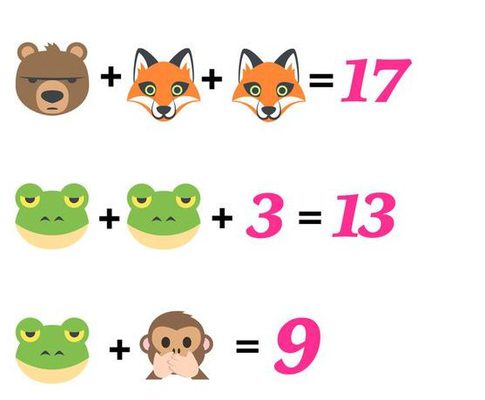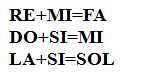Algebrogramy - klasické matematické hlavolamy • Mozkolam.cz

2.6

(22)

Co je to algebrogram?

Algebrogram je úloha, jejíž řešení spočívá v náhradě zadaných znaků (písmen či jiných symbolů) číslicemi tak, aby zadané početní úkony dávaly korektní výsledek. Stejné znaky musí být nahrazeny stejnými číslicemi, různé znaky různými. Žádné číslo (kromě nuly) nezačíná číslicí nula. Algebrogram může obsahovat speciální symboly, které se nahrazují číslicemi z nějaké množiny, např. hvězdička či tečka pro libovolnou číslici, S pro sudou číslici, P pro prvočíslo (2, 3, 5, 7) apod. Stejné speciální symboly mohou být nahrazeny různými číslicemi. Použití těchto symbolů bývá v zadání zpravidla vysvětleno.

Typy algebrogramů

Nejčastěji se setkáváme s těmito typy:
1. Devět čísel v rastru 3 x 3 zapojených do šesti rovnic − jedna v každém řádku a jedna v každém sloupci. U tohoto typu bývá časté zadání pomocí různých symbolů (viz příklady 1 – 3). Někteří autoři považují za algebrogram pouze tento typ, v dalším textu budeme takové úloze říkat klasický algebrogram.
2. Součet několika čísel, zpravidla ve formě smysluplného textu (viz příklady 4 – 7).
3. Součin nebo podíl rozepsaný do tvaru ručního násobení či dělení. V rovnici máme tedy ukryto několik součinů a součtů. Speciální symboly se nejčastěji vyskytují právě u tohoto typu (viz příklady 8 – 11).
Algebrogram může obsahovat tajenku, pokud seřadíme písmena podle nahrazených číslic, zpravidla (ale ne vždy) ve vzestupném pořadí 0 až 9.

Příklady:

Klasický algebrogram s tajenkou

Algebrogram s jinak ukrytou tajenkou

Symbolický anagram

Rozumně neřešitelný algebrogram

Pravdivý součet

Řešitelný součet

Tři hudební rovnice

Sudá a lichá

Formule 1

Jak řešit algebrogramy

Obecný návod na řešení algebrogramů neexistuje. Každá úloha mívá v sobě slabé místo, které je potřeba objevit a od toho místa začít s řešením. Snad jenom u klasického algebrogramu (viz níže řešený příklad úlohy č. 1) lze použitý postup použít na většinu příkladů. U některých úloh žádný rozumný postup neexistuje a je potřeba víceméně projít všechny možnosti, dokud nenajdeme řešení. Jedná se hlavně o úlohy druhého typu, kdy autor na počítači zkouší, zda náhodou PETRA + JEDE + DO = PRAHY nemá jediné řešení a pokud ano, tak ji publikuje nebo použije v soutěži bez ohledu na to, zda je rozumně řešitelná. Všechny výše prezentované úlohy (kromě Petry jedoucí do Prahy) jsou dobře řešitelné.

Kde začít?

V úlohách bývá několik typických míst, kde se dá začít. Mnoho může napovědět délka (počet číslic) jednotlivých čísel. Je-li součtem dvou dvouciferných čísel číslo trojciferné, pak toto musí začínat jedničkou. Např. LA + SI = SOL (L = 1) nebo podobně PAN + KNP = PYPS (P = 1). Ze součtu ABC + DE = FGHI dokonce plyne A = 9, F = 1 a G = 0. Z rovnice IR + KNP = EYI sice nevykoukáme žádnou konkrétní hodnotu, ale víme, že K + 1 = E.
Kromě prvních číslic je užitečné, ne-li užitečnější, sledovat poslední číslice. Poslední číslice součtu dvou čísel závisí pouze na poslední číslici sčítanců. Totéž platí pro rozdíl a součin. Pro podíl tato vlastnost neplatí! V níže řešených příkladech jde o jeden z nejčastěji používaných kroků, proto pro něj zavedeme speciální symbol. Zápis A + B ≡ C bude znamenat, že poslední číslicí součtu A + B je číslice C. Např. 8 + 9 ≡ 7 nebo 3 × 8 ≡ 4.
Je dobré si všímat míst, kde se víckrát opakuje jedno či dvě písmena. Pokud poslední číslice v součtu dávají vztah A + B ≡ A, pak B musí být nula. Např. DO + SI = MI dává O = 0. Podmínka A × A ≡ A má čtyři možnosti (0, 1, 5, 6) a dvě současně platící podmínky B × B ≡ A a A × B ≡ B dávají jenom dvě možnosti (najděte je sami).

Najděte nulu

U klasických algebrogramů, které používají všech deseti číslic (tj. v zadání je deset různých písmen či jiných symbolů), můžeme dost často určit nulu. Nulou nesmí začínat žádné víceciferné číslo a poslední číslice sčítanců a činitelů můžeme většinou jako nulu taky snadno vyloučit. Např. v úloze č. 1 můžeme rovnou vyloučit devět možností a zůstává pouze možnost S = 0.
Někdy může být užitečné si všímat parity (sudosti a lichosti) jednotlivých číslic. Součet je sudý, pokud jsou oba sčítanci sudí nebo oba liší. Součin je lichý, pokud oba činitelé jsou liší. Např. v úloze č. 2 už víme, že P = 1. Z rovnice v prvním sloupci PS × IR = SRP odvodíme, že S i R jsou liché. A z rovnic ve třetím řádku a druhém sloupci (P + S ≡ K, N + P ≡ S) lze odvodit, že K a N mají stejnou paritu. Při řešení této konkrétní úlohy to sice nepomůže, ale u jiných úloh to může být klíčová myšlenka vedoucí k rychlému vyřešení.
Zběhlí matematici by se mohli snažit řešit algebrogramy pomocí soustav rovnic. Klasický algebrogram je vlastně soustava šesti rovnic o devíti neznámých, u dalších typů můžeme vytvořit rovnice přímo z číslic − např. RE + MI = FA lze matematicky zapsat jako (10 × R + E) + (10 × M + I) = (10 × F + A). Vězte, že tento postup je v naprosté většině případů ztrátou času a k cíli nevede. Výjimka ovšem potvrzuje pravidlo a k efektivnímu vyřešení úlohy č. 10 se hodí sestavit a prozkoumat jednu rovnici.
Zdroj: Český svaz hádankářů a křížovkářů https://www.cshak.cz